1.4. 移動平均 #
1.4.1. 機能概要 #
カラムごとに移動平均処理を適用し、平滑化します。
時系列データの誤差変動が大きい場合、変化のパターンを読みやすくするために時系列変動の平滑化を行い誤差変動をキャンセルアウトすることが有効です。
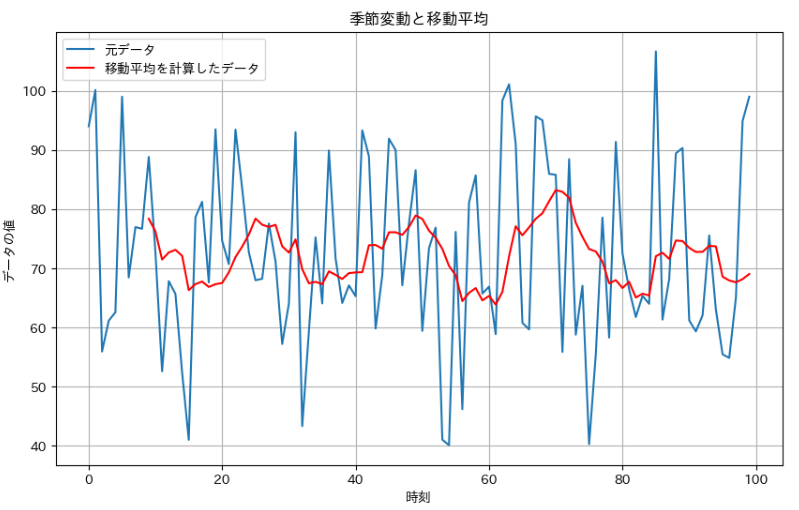
例えば、下図の折れ線グラフは横軸の時刻に対してある値を縦軸にプロットしたダミーデータです。青色のグラフが元のダミーデータで、赤色のグラフは移動平均を計算したあとのデータを表しています。
移動平均を計算する前は上下の変動が激しく、長期的に見てどのタイミングで値が上下するのかがわかりづらくなっています。このようなデータのとき、赤色の折れ線グラフのように移動平均を計算すると、グラフの変動が小さくなり、中長期的な変動がわかりやすくなります。
1.4.2. 入力と出力 #

| 種別 |
|---|
| データ |

| 種別 |
|---|
| データ |
1.4.3. 操作方法 #
1.4.3.1. 結線 #
処理対象データを結線してください。
1.4.3.2. パラメータの設定 #
1.4.3.2.1. パラメータの設定 #

| 設定項目 | 説明 | 初期値 |
|---|---|---|
| 窓位置 | 移動平均の算出方法 | 後方移動平均 |
| 窓幅(レコード数) | 移動平均の適用幅 | |
| ※適用カラム | 移動平均適用の対象カラム |
-
後方移動平均(推奨)
- 移動平均処理を適用したカラムは、対象の時点を除いた窓幅分が失われます。移動平均を適用していないカラムを含め、全てのカラムの長さが短くなります。
- 「後方移動平均」は一般的には「移動平均」と略されることが多いです。
-
中央移動平均
- 移動平均処理を適用したカラムは、対象の時点の前後それぞれ窓幅の約半分が失われます。移動平均を適用していないカラムを含め、全てのカラムの長さが短くなります。
- 予測のときには リークになる可能性があるので、設定する場合には注意が必要です。
※「適用カラム」は処理データに結線した際に現れます
1.4.3.2.2. 移動平均の計算方法 #
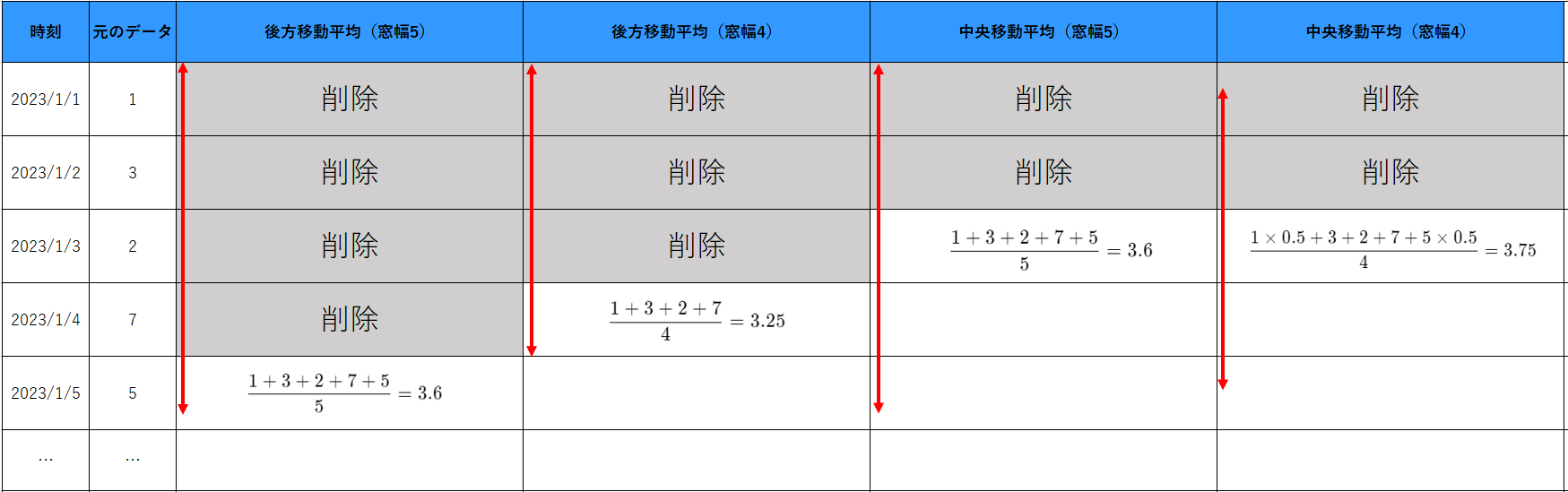
移動平均の計算方法は「後方移動平均」と「中央移動平均」でそれぞれ異なります。次の5つのデータで具体的な計算方法を紹介します。
※中央移動平均の窓幅が偶数の場合、窓の両端の数は1/2倍されます。
つまり、後方移動平均の窓幅が5の場合は
\[\overline{x_5}=\dfrac{x_1+x_2+x_3+x_4+x_5}{5}\] と計算します。
また、中央移動平均の窓幅が奇数(窓幅5)の場合は
\[\overline{x_3}=\dfrac{x_1+x_2+x_3+x_4+x_5}{5}\]のように計算し、窓幅が偶数(窓幅4)の場合は \[\overline{x_3}=\dfrac{x_1 \times 0.5 +x_2+x_3+x_4+x_5 \times 0.5}{4}\] と計算します。
1.4.3.2.3. 移動平均の適切な窓幅 #
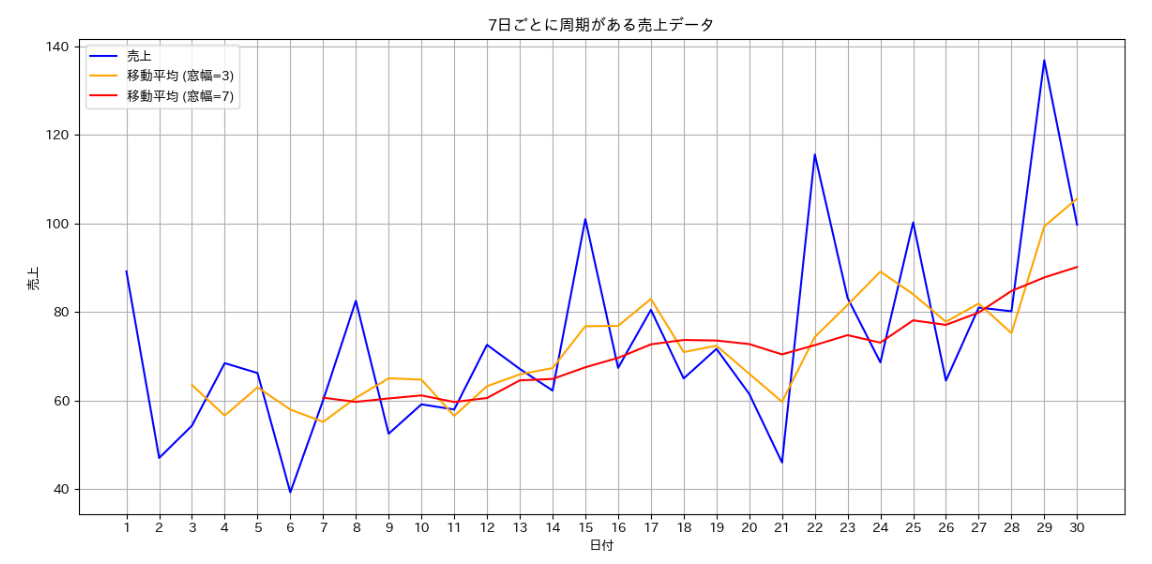
データによって適切な窓幅は異なりますが、一般的にはそのデータの周期を見極めそれに合わせた窓幅を設定することで適切に変動の平滑化ができ、中長期的な変動を抽出することができます。
例えば、下図の1か月の売上データは、中長期的には上昇傾向があり7日ごとの周期をもつダミーデータです。窓幅が3の移動平均(橙色)と窓幅が7の移動平均(赤色)を比較すると、周期に合わせた窓幅7の移動平均の方がより適切に平滑化され、中長期的な変動が抽出できていることがわかります。
1.4.3.3. 実行 #
- パラメーターに従い移動平均処理が行われます
- 処理が成功すると、メッセージが表示されます
- 処理された件数が表示されます
- 先頭行か末尾の行に外れ値が含まれている場合は、直前/直後の値が存在しないため、エラーになります
- 処理時間が 10 分を超えるとタイムアウトし、処理が強制終了されます。
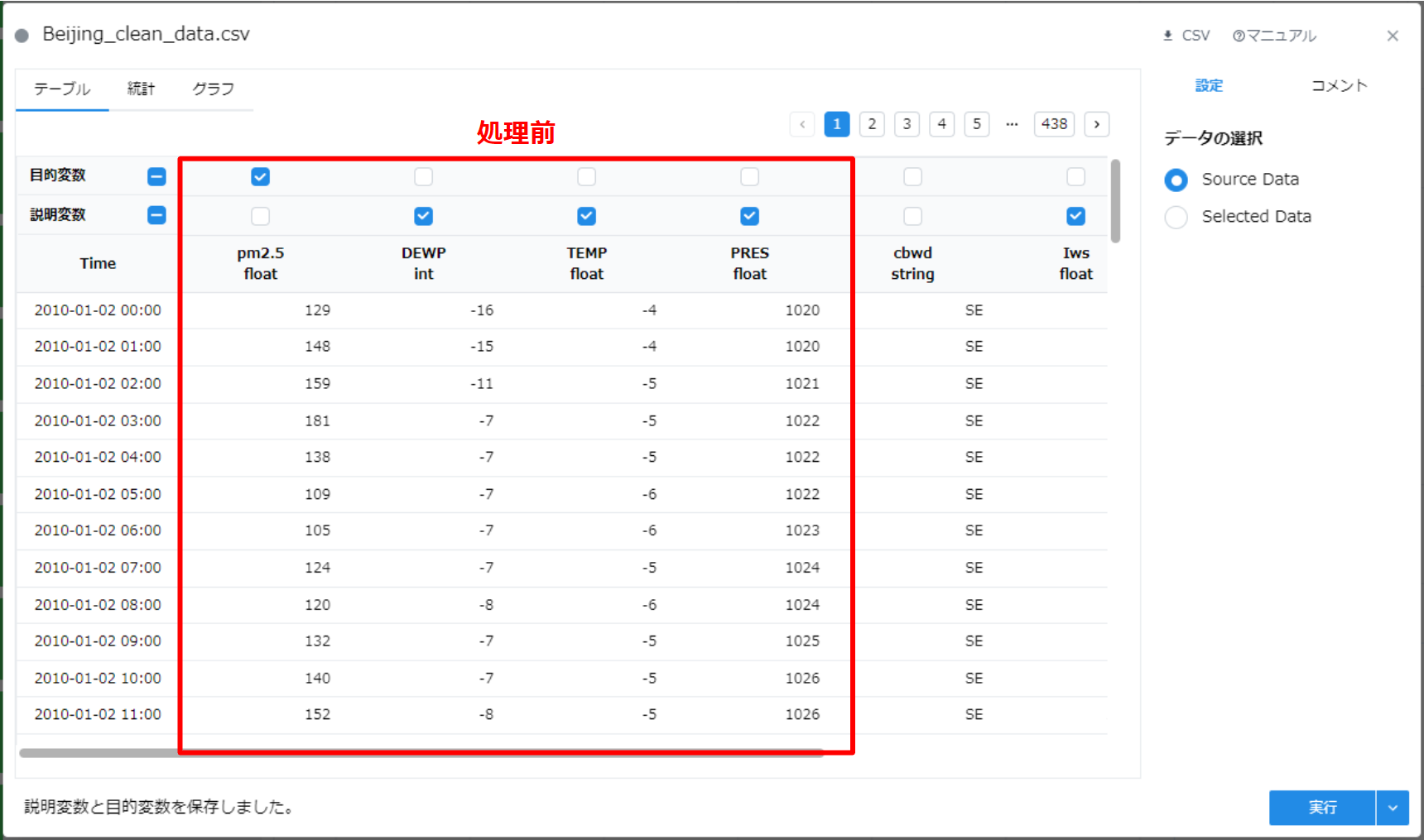
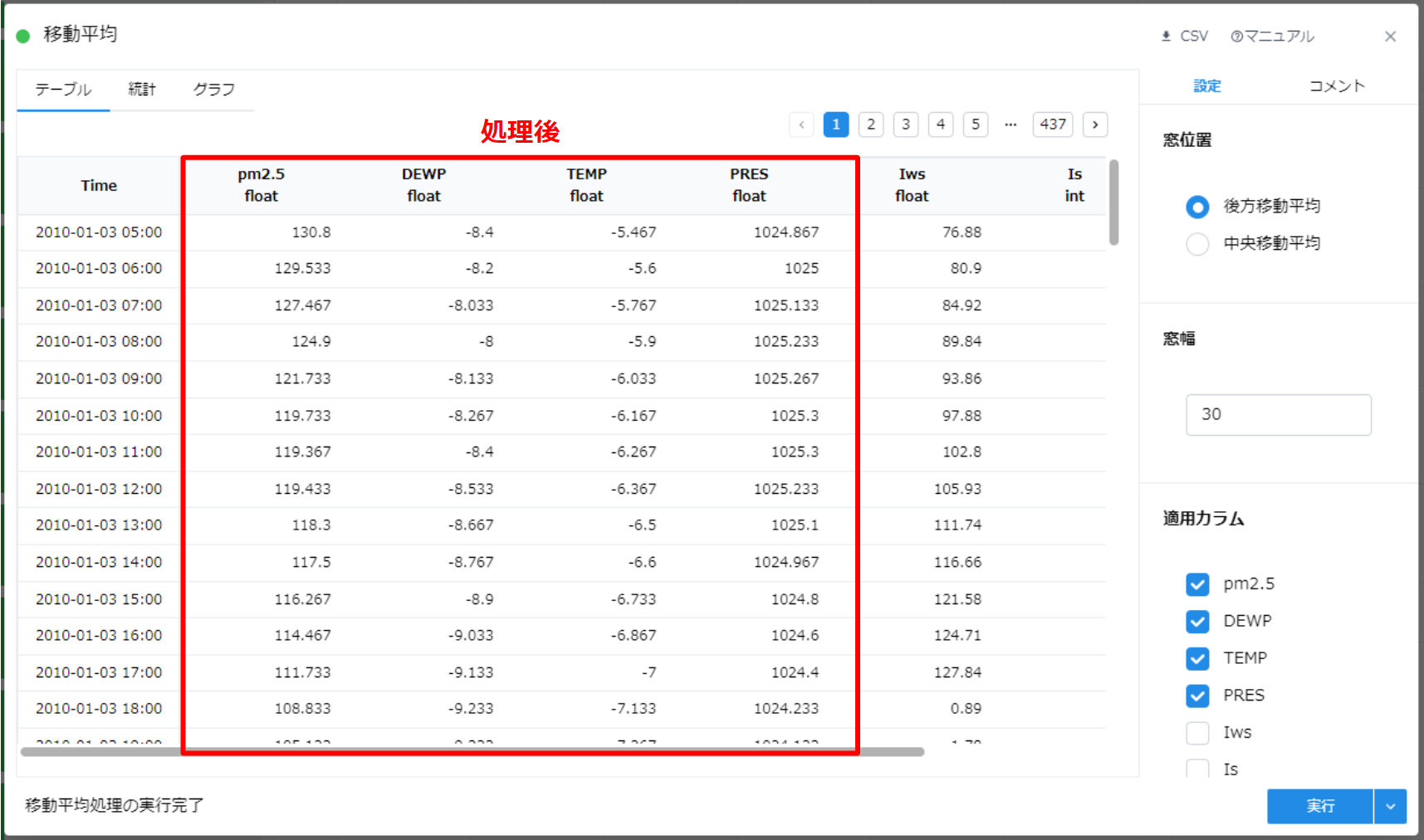
1.4.3.4. 処理結果の確認 #
- 必要に応じて、表形式、統計量、グラフ形式で分割結果を確認してください